Una idea general

¿Qué es el Triángulo de Pascal?

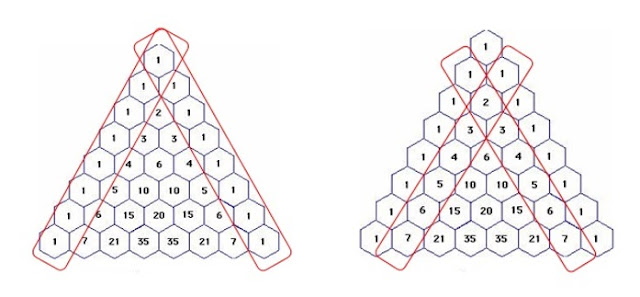
   Triángulo de Pascal (con números). 

   
Podemos definirlo como una disposición de números con forma de triángulo, construida de tal manera que cada elemento es la suma de los dos inmediatamente superiores a él, y donde inicialmente se coloca el número 1 en los lados exteriores.


Teniendo en cuenta la definición podemos construir el triángulo de la siguiente manera:

Para ponernos en contexto

Historia

Las primeras descripciones de este triángulo datan del 1100 d.C., durante la Edad Media Oriental, con matemáticos chinos que posiblemente se basaron en fuentes indias y chinas más antiguas. En ese año, el matemático Chia Hsien lo define comoSistema de Tabulación para calcular coeficientes de binomios, dada la correspondencia que existe entre el Triángulo de Pascal y los coeficientes del desarrollo del binomio de Newton. Ese fue el origen de diversos estudios sobre este triángulo en este parte del mundo, pero no fue hasta la segunda mitad del s. XVI que fue dado a conocer en Europa, con el matemático alemán Michael Stifel y su obra Arithmetica integra (1544).

Posteriormente, entre 1556 y 1560, el estudio de una disposición numérica similar aparece en las obras del matemático italiano Niccolo Fontana, también conocido como Tartaglia.

Blaise Pascal, el gran matemático, físico y filósofo francés, es el primero en relacionar rigurosamente el Teorema del Binomio con los números combinatorios, y publicó en 1665 un tratado en el cual deduce nuevas propiedades y aplicaciones del triángulo aritmético a la Teoría Combinatoria. En honor a sus aportes fue que el matemático escocés George Chrystal, en 1886, lo denomina Triángulo de Pascal en su obra Álgebra.

El Triángulo de Pascal y el número π (Pi)

Tomemos la diagonal de los números triangulares y pongamos a los impares a sumar y a los pares a restar, es decir 1+3-6-10+15... y así. Ahora reemplazamos cada número con su inverso, es decir (1/1)+(1/3)-(1/6)-(1/10)+(1/15)... y así, luego esa suma infinita más 2 es igual a Pi.

[C++] Coeficientes binomiales | Triángulo de Pascal

A continuación para los amantes del Dev C++ dejamos un vídeo que muestra el código de como realizar el Triángulo de Pascal utilizando los coeficientes binomiales.

Triángulo de Pascal vs Triángulo de Sierpinski

¿Qué relación tienen los dos triángulos? 

El triángulo de Sierpinski es un fractal que se construye a partir de un triángulo cualquiera. Si unimos los puntos medios de cada lado obtenemos un triangulo dividido en cuatro triángulos. Luego eliminamos el triangulo central de color blanco; y a partir de eso repetimos el proceso con los otros tres triángulos de color negro y así de manera indefinida. 

El resultado es una figura con la cualidad de que una pequeña parte de ella es igual a la totalidad de la figura.

Proceso del triángulo.

Ahora si nos fijamos en el triángulo de Pascal y eliminamos los números pares, el triángulo cumple el mismo patrón que el triángulo de Sierpinski.

Números Poligonales

Las primeras diagonales de la izquierda y la derecha son nada mas que unos. Las segundas forman la sucesión de números naturales.

                        Primeras diagonales.                                                                     Segundas diagonales.                

En la tercera diagonal aparecen los números triangulares, son aquellos que pueden recomponerse en un triángulo equilátero.

Los números cuadrados se encuentra en el triángulo de Pascal recurriendo a la misma diagonal que en el caso anterior: construimos cada uno sumando dos números triangulares consecutivos. Eso nos proporciona: 1, 4, 9, 16, 25, ...

                               Números triangulares.                                             Números cuadrados:1+3=4, 3+6=9, 6+10=16 ...

Sucesión de Fibonacci

La serie de Fibonacci puede ser encontrada en el triángulo de Pascal. Dividiendo al mismo según las líneas que mostramos en el diagrama.

Recordemos que esta sucesión se construye sumando a cada número su anterior para obtener el siguiente, entonces si el primer número es un 1 su anterior será el 0 y su siguiente 0+1, es decir 1, entonces tendremos "1,1" luego 1+1 es 2 y 1+2=3 por lo que siguiendo esta lógica nos queda 1,1,2,3,5,8,13... y así sucesivamente.

 Sucesión de Fibonacci en el Triángulo de Pascal

                                   
             


                                       

Los secretos del TRIÁNGULO DE PASCAL

Si bien en este blog nos expresamos textualmente, ¿qué mejor que un video para darnos otra perspectiva?

Biografía de Blaise Pascal

Nacido en Clermont (Francia), quedó huérfano de madre a los 3 años. En 1632 se trasladó a vivir a París. El padre de Pascal tenía unas opiniones poco ortodoxas sobre la educación, por lo que él se dedicaba a enseñar a su propio hijo. Unas de dichas opiniones era que Pascal no debía estudiar matemáticas, pero esto produjo en Pascal curiosidad que le llevó a estudiarlas a espaldas de su padre.


En 1639 la familia Pascal se trasladó a vivir a Rouen, donde habían destinado al padre como recaudador de impuestos.Para ayudar a su padre en su trabajo, Pascal inventó uno calculadora mecánica. Trabajó varios años en este proyecto hasta perfeccionarla, a la máquina se la conoció como la Pascalina. Se construyeron y comercializaron varios ejemplares de la máquina que estaba pensada para cálculos con la moneda francesa. Esto hace que Pascal fuera la segunda persona tras Schickard en inventar una calculadora mecánica. 

La Pascalina

Otro de los campos en los que estudió Pascal fue la física, y más concretamente sobre la presión atmosférica publicando en 1653 el Tratado sobre el equilibrio de líquidos.
En 1654 formuló, junto con Pierre de Fermat, la teoría matemática de la probabilidad.
Pascal fue un hombre profundamente religioso, y esto se reflejaba es sus trabajos filosóficos, como el que publicó en 1656 Pensées, en donde dice: "Si Dios no existe, uno no perderá nada creyendo en él, mientras que si él existe, uno perderá todo por no creer".





Breve resumen de la vida de Blaise Pascal

 

Suma de Potencias

Hay una serie de combinaciones que nos entrega el Triángulo de Pascal, donde cada número es la suma de los dos números que se ubican a los costado del triángulo.

Como vemos, la suma de los números de cada piso del triángulo corresponde a las potencias de 2. Pero el triángulo también nos sirve para determinar los coeficientes de los polinomios resultantes de las potencias de un binomio cualquiera, hacemos (1 + 1) ⇒ (a + b) y nos queda:

El "stick de hockey"

Si tomamos cualquier diagonal que empiece en un extremo del triángulo, y de la longitud que sea, cumple que la suma de todos los números que la integran se encuentran justo debajo del último de ellos, en la diagonal contraria. Podemos ver dos ejemplos en la siguiente imagen:

Fuentes

Por Débora Jaqueline Strigman:

Armendáriz, David (Diciembre 2016). Codigo C++ del Triángulo de Pascal. Accedido el 12 de junio de 2018 desde https://youtu.be/HMyp50jOI8g

Murillo Díaz, Miguel Angel (Noviembre 2011). Triágulo de Sierpinski. Accedido el 11 de junio de 2018 desde https://cienciaytecnica.blogia.com/2011/110401--hr-el-triangulo-de-pascal-y-el-triangulo-de-sierpinski.php



Burrull Naredo, Gastón Rafel. (Marzo  2009). Suma de Potencias. Accedido el 25 de Mayo de 2018 desde http://www.lawebdefisica.com/files/arts/Suma%20de%20Potencias.pdf


Saénz de Cabezón, Eduardo. (Mayo  2017). Los secretos del TRIÁNGULO DE PASCAL. Accedido el 29 de Mayo de 2018 desde https://www.youtube.com/watch?v=DPxIbJ-Rbf4&t=2s

Por David Carvallo:

R. Podestá, P. Tirao. (Marzo 2014)Álgebra, una introducción a la Aritmética y a la Matemática Discreta. Accedido el 20 de Mayo desde http://www.famaf.unc.edu.ar/wp-conten  t/uploads/2014/03/NotasAlgebra2014.pdf


mashupHistory(canal de youtube).(Junio 2014). Blaise Pascal. Accedido el  21 de Mayo de 2018 desde https://www.youtube.com/watch?v=iybEqlQSk_E

 Aznar Enrique R.(2007).Niccolo Fontana (Tartaglia), Matemático (1499 Brescia, república de Venecia, 1557 Venecia, actualmente Italia). Accedido el 23 de Mayo de 2018 desde https://www.ugr.es/~eaznar/tartaglia.htm


Jesús Soto.(Mayo 2016).El “stick de hockey”. Accedido el 24 de Mayo de 2018 desde http://pimedios.es/2016/05/25/el-stick-de-hockey/